Matematičarka izračunala što Hrvatsku čeka protiv Nigerije
MATEMATIČARKA, doc. dr. sc. Franka Miriam Brueckler sa zagrebačkog PMF-a, već godinama radi na popularizaciji znanosti, a jedna od najdražih tema joj je matematička (ne)predvidivost nogometa.
Kako se bliži prva hrvatska utakmica na ovogodišnjem Svjetskom prvenstvu, za Index je pokušala prognozirati njezin ishod i usto objasniti kako se predviđanja rade.
Evo što kaže.
Prvo pitanje je koliki period uzeti za statističke podatke – ne smije biti predug da podaci ne bi postali irelevantni (kakve veze hrvatski rezultati iz 1998. imaju s još nepoznatim rezultatima na ovogodišnjem SP-u?), ali ne ni prekratak jer bi u tom slučaju bilo premalo podataka da bismo iz njih mogli išta zaključiti. Uzmimo, primjerice, da gledamo državne utakmice Hrvatske i Nigerije tijekom 2017. i 2018.
Hrvatska je od 1. 1. 2017. odigrala 16 utakmica. Ukupno je dala 16 golova i primila njih 15. Drugim riječima, davala je u prosjeku 16/16 = 1 gol, a primala 15/16 = 0,94 po utakmici. Kada ne bismo imali nikakvih drugih podataka, kao najvjerojatniji rezultat sljedeće utakmice naših kvadratićastih (nisu kockasti!) mogli bismo pretpostaviti 1:1.
No, naravno, predstojeći rezultat ovisi i o protivniku. Ove subote to je Nigerija. Ona je u istom razdoblju odigrala 18 utakmica (od čega 5 prijateljskih) i dala je 19, a primila 17 golova, odnosno prosječno je po utakmici davala 1,06 golova, a primala 0,94 gola. Dakle, i kad bismo gledali samo iz perspektive Nigerije, razumno bi bilo kao najvjerojatniji rezultat predvidjeti 1:1. U tablici su prosjeci danih i primljenih golova tijekom 2017. i 2018. za sve 4 momčadi naše grupe:
Naravno, svatko može lako vidjeti da ovdje neke stvari nismo uzeli u obzir. Primjerice, nameće se pitanje trebamo li rezultate prijateljskih utakmica uzimati kao jednako važne? Ako ih zanemarimo, broj podataka se smanjuje pa su manje pouzdane procjene, a opet, svakom je jasno da nije ista situacija kad momčad igra prijateljsku i službenu utakmicu. Ipak, jednostavnosti radi, ovdje ćemo to zanemariti te, isto kao i teško brojevima opisive parametre (bolesti ključnih igrača, eventualne afere i sl.), prepustiti osjećaju.
Kako se 1:1 i iz perspektive Hrvatske i iz perspektive Nigerije čini vjerojatnim rezultatom, mogli bismo uzeti taj rezultat kao najvjerojatniji. No ovo je samo početak priče, a za nastavak zapravo nije važno što je eto slučajno iz perspektive obje momčadi isti rezultat ispao vjerojatan.
Koliko je vjerojatan taj naš “najvjerojatniji” rezultat? A koliko je vjerojatan bilo kakav neodlučeni rezultat? Detaljan odgovor na ova i slična pitanja nije moguć u ovako kratkom članku, ali evo bar nekoliko osnovnih ideja.
Za procjene vjerojatnosti konkretnih rezultata koriste se razni modeli, čiji temelj je tzv. Poissonova razdioba. U svojoj najjednostavnijoj formi ona kaže: Ako neka momčad u prosjeku daje N golova po utakmici onda je vjerojatnost da će ih dati K jednaka N^K/K!e^N (pritom ^ označava da se broj prije njega diže na potenciju koja slijedi iza znaka – N na K, a znak ! je oznaka za faktorijel). Za one koji ne znaju što znači ova formula: slobodno zanemarite – svaki bolji kalkulator bez problema će vam izračunati vjerojatnost da će momčad koja u prosjeku daje 1,06 golova (npr. Hrvatska) na sljedećoj utakmici s bilo kim zabiti točno 2 gola. Trebate samo u kalkulator upisati 1^2/(2!e^1) i dobit ćete rezultat od 0,1839, odnosno 18,39 %.
Ako želimo procijeniti vjerojatnost rezultata, primjerice, 2:1, trebamo pomnožiti vjerojatnosti da prva momčad zabije 2, a druga 1 gol. Zapravo, vjerojatnosti se smiju množiti samo ako se odnose na nezavisne događaje, što ovdje nipošto nije slučaj, no uzimanje u obzir međuovisnosti jako bi kompliciralo model, bez velikog povećanja pouzdanosti procjene. Tako za utakmicu Hrvatska – Nigerija vjerojatnost rezultata koji smo nazvali najvjerojatnijim, 1:1, ispada samo 13,51 %! Kao što vidimo, čak i najvjerojatniji rezultat nije jako vjerojatan. Naime, s obzirom na prosjeke, dosta su vjerojatni i rezultati 0:0, 1:0, 0:1, te se zbrajanjem vjerojatnosti tih rezultata može dobiti da je vjerojatnost da ni Hrvatska ni Nigerija ne daju više od jednog gola oko 51 %. No ne treba zanemariti ni sve ostale moguće rezultate.
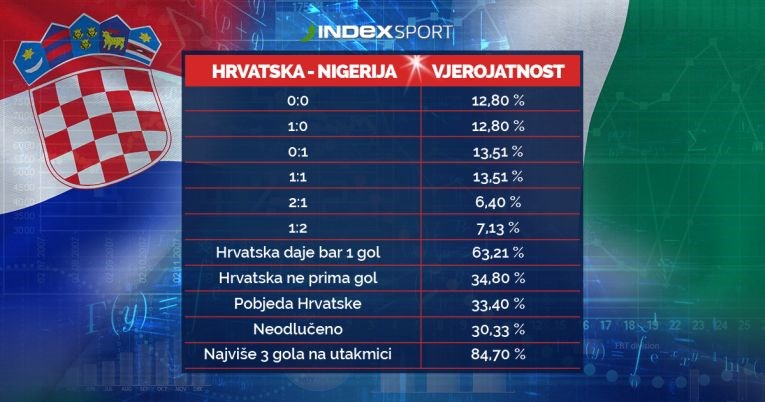
Evo tablice ovako dobivenih procjena nekih vjerojatnijih mogućnosti za razvoj situacije 16. lipnja uvečer:
U tablici su kompliciranije vjerojatnosti dobivene zbrajanjem vjerojatnosti pojedinih mogućih rezultata. Recimo, vjerojatnost pobjede Hrvatske dobiva se kao zbroj vjerojatnosti svih rezultata 1:0, 2:0, 3:0, ..., 2:1, 3:1, ..., 3:2, ...
Ovo gore opisano, naravno, samo je pojednostavljena verzija ovakvih izračuna, no glavne razlike između “profesionalnih” i naših “laičkih” procjena su u metodama procjene broja golova koje momčadi primaju i daju (postoje načini razlikovanja uloge domaćin i gost, uzimanja u obzir čitave lige u kojoj momčadi igraju i sl.) te prilagodbama našeg osnovnog modela Poissonove razdiobe dodatnim podacima i uočenim trendovima.
Uzimajući u obzir neke druge parametre, o kojima će više riječi biti prije drugih utakmica, Miriam Brueckler predviđa da bi pobjeda Hrvatske u subotu mogla biti vjerojatna s više od 60 %, a rezultat 1:0 oko 15%.
Draž nogometa je u nepredvidivosti
Ovdje se ipak nameće jedno puno važnije pitanje od pitanja možemo li preciznijim modelom rezultat procijeniti s 13,51 % umjesto s 9,44 %. To je pitanje koliko su ovako dobivene procjene uopće pouzdane?
Jedna od velikih čari nogometa je, kao što svi iz iskustva znamo, da je vrlo nepredvidiv. To nije samo subjektivni osjećaj – 2006. godine znanstvenici iz Los Alamos National Laboratory (New Mexico, SAD) statističkom su analizom usporedili rezultate više od 300.000 utakmica “običnog” i američkog nogometa, hokeja, košarke i baseballa te su pokazali da je nogomet najkompetitivniji. Neočekivani rezultati tipa ''slabiji pobijedio boljeg'' u nogometu europskog stila znatno su češći nego u ostala četiri sporta. Drugim riječima, mnogo je teže kladiti se na rezultate nogometnih utakmica nego, primjerice, na one iz košarke. To se može objasniti i teorijski, no o tom nekom drugom prilikom.
Pouka ove priče jest: Matematika (konkretno, statistika i vjerojatnost) mogu čak i laiku pomoći da dobije smislene brojeve kao procjene vjerojatnosti nogometnih utakmica, no i s najpouzdanijim metodama ostaje pitanje sreće, slučajnosti, sposobnosti. Pa tko bi se inače živcirao ili stvarno veselio tijekom SP-a kad bi se rezultati mogli pouzdano predvidjeti? Stoga je jedini točan odgovor na pitanje iz naslova: Samo ako imate dokazano funkcionirajuću kristalnu kuglu.
P. S. Za one koji se klade: Koeficijenti u kladionici su recipročne vrijednosti vjerojatnosti koje kladionica procijeni (i prilagodi svom cilju zarade). Ako, primjerice, za rezultat 1:1 i kladionica nudi koeficijent 6,30, znači da su oni procijenili vjerojatnost tog rezultata s 1/6,30 = 15,87 %, dok bi naša procjena 13,51 % značila koeficijent 1/0,1351 = 7,40. U prijevodu, naš račun je pokazao da je tu kladionica dala puno slabiji koeficijent od izračunatog (vjerojatnije je da su dobili sličan rezultat kao mi i onda oslabili koeficijent jer će se puno ljudi kladiti pa da u slučaju tog rezultata profitiraju, osiguravaju se slabljenjem koeficijenta). Stoga je bolje naći neku okladu za koju je kladionički koeficijent bliži izračunatom; rijetko će se dogoditi da je bolji od izračunatog.































 Facebook
Facebook
 Google
Google